Been on the Reddit forums or speedcubing YouTube recently and seen mentions of a new method named the "Mehta" method. What is it, and is it better than the big three methods, CFOP, Roux, and ZZ? Read more to find out.
Introduction
Proposed by Yash Mehta in 2020, the Mehta method relies on high algorithm usage, similar to ZZ, which has the effect of high TPS. Unlike CFOP, the method also has a lower average move count in comparison, similar to the move count of Roux.
For "full Mehta", known as Mehta-OS, OS standing for Option Select, the solver must know enough of the algorithms from four different "paths"
Pronunciation
Steps
First Block (FB)
Solve a 1x2x3 block on the D layer
3 Quarters Belt (3QB)
Solve 3 E-Slices
Edge Orientation & Last Edge (EOLE)
Insert the final E-slice edge and orient all edges at the same time.
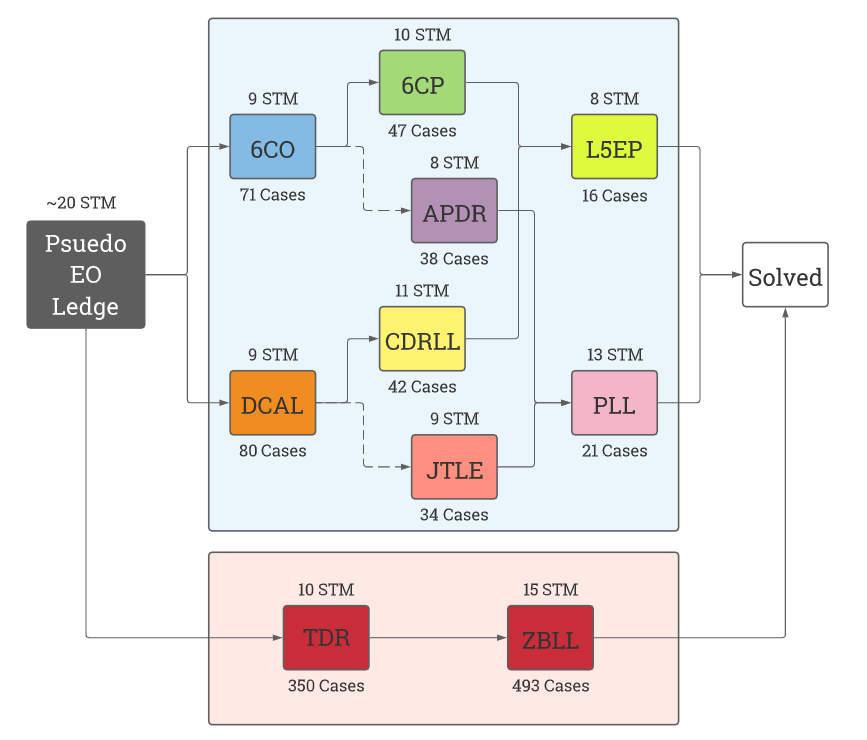
Option Select
One of five major paths can be used to solve the rest of the cube
| Mehta-6CP (6 Corner Pemutation) | Mehta-APDR (Andreas' Permutation of DR block) | Mehta-CDRLL (CxLL, Corners of Last Layer, with down-right edge, DR, unsolve) | Mehta-JTLE (John Tamanas Last Edge) |
| Orient the 6 corners | Orient the 6 remaining corners | Solve the 2 Corners of the D layer | Solve the 2 corners of the D layer |
| Permute the corners | Solve the DR block (corners and edges) | Orient and permute the U layer corners (COLL) | Orient the U layer corners and insert DR edge |
| Solve the last 5 edges | Solve the top layer (PLL) | Permute last 5 edges | Solve the top layer using 21 algorithms |
There is a final Mehta option, Mehta-TDR, which involves solving the final DR block, and then solving the U layer with ZBLL, which consists of 843 algorithms, which may be unrealistic for a human to learn to is not considered in Mehta-OS, OS standing for Option Select, where the best "path" or final steps are chosen. Solvers are advised to default to CDRLL path if there are not any good options.
Source: https://devagio.github.io/Mehta/index.html
Should you learn Mehta?
Mehta boasts a rotationless and high turns per second, TPS, solving style in exchange for learning a lot of algorithms. A lower movecount is also a great selling point, but it may be difficult for current CFOP users especially to learn both how to block-build for Mehta's first step and the heavy algorithm reliance. However, for dedicated cubers the Mehta method could in theory be high speed, fast time producing method - however time will tell whether this method gains popularity and is actually viable in WCA competition.
Resources
https://www.speedsolving.com/wiki/index.php/Mehta
https://www.reddit.com/r/Cubers/comments/jyya9c/the_mehta_method/





























